 Índice |
Índice |  III. Probabilidade |
III. Probabilidade |  V. Exercícios
V. Exercícios
IV. Modelos de Probabilidade discretos e contínuos
Parte 56 de 78
Modelos de probabilidade discretos
|
O Problema das Caixas de Cereais - Resolução por simulação (cont.) |
|||
|
|
|||
|
No gráfico seguinte apresentamos a evolução da média dos resultados anteriores, à medida que o n.º de experiências aumenta: Ao fim da realização das 200 experiências obtivémos o valor de 14.88 para a média do número de caixas que é necessário comprar até se obter todos os prémios. Este valor é uma estimativa do valor médio (que neste caso é conhecido e igual a 14.7). Se aumentássemos o número de experiências, obteríamos uma estimativa mais precisa. A justificação para este facto é dada pela lei dos grandes números.
|
|||
|
Nota – Na parte 46 utilizou-se outro processo para simular o lançamento de um dado equilibrado, através da função Randbetween(a;b) [AleatórioEntre(a;b)]. |







 Para cada experiência, fomos verificar quantos lançamentos teriam sido necessários para obtermos os 6 números distintos, de 1 a 6, obtendo uma amostra de dimensão 200, que pode ser considerada como a observação da variável aleatória, que representa “o n.º de caixas que é necessário comprar até termos os prémios todos”, 200 vezes. Apresentamos a seguir, os resultados obtidos:
Para cada experiência, fomos verificar quantos lançamentos teriam sido necessários para obtermos os 6 números distintos, de 1 a 6, obtendo uma amostra de dimensão 200, que pode ser considerada como a observação da variável aleatória, que representa “o n.º de caixas que é necessário comprar até termos os prémios todos”, 200 vezes. Apresentamos a seguir, os resultados obtidos: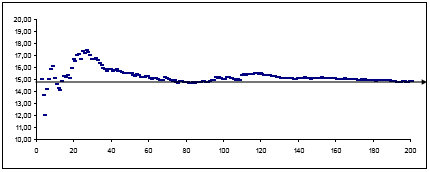





.png)
