Este sítio utiliza cookies

Estes cookies são essenciais quer para melhorar as funcionalidades quer para melhorar a experiência de utilização do sítio ALEA.

Imprimir

NOÇÕES DE PROBABILIDADES

Índice | III. Probabilidade | V. Exercícios

IV. Modelos de Probabilidade discretos e contínuos

Parte 60 de 78

Modelos de probabilidade discretos

Será que estamos em condições de modelar a situação através do modelo Binomial? Não, se pensarmos estritamente nas condições exigidas para aplicação do modelo, nomeadamente quando se exige que as “selecções” ou provas, sejam independentes e a percentagem de sucesso seja constante, de prova para prova. Neste caso, ao seleccionarmos o primeiro dos 20 alunos que constituem a amostra, a probabilidade de sucesso é igual a 3227/5564, mas após esta primeira selecção, a composição da população, no que diz respeito à percentagem de sucessos quando se vai seleccionar o 2º aluno, vem alterada, já que será igual a 3226/5563 ou 3227/5563, conforme o primeiro aluno seleccionado foi rapariga ou rapaz, respectivamente. No entanto estes valores são tão próximos, que na prática podemos dizer que o facto de termos retirado um elemento da população, não alterou a sua composição. O mesmo raciocínio pode ser feito para as selecções seguintes.

Se na experiência anterior, a dimensão N da população, de onde foi recolhida a amostra, sem reposição, fosse suficientemente grande, relativamente à dimensão n da amostra recolhida, então a probabilidade de sucesso não sofreria alterações significativas de prova para prova.

Nestas condições podemos ainda utilizar o modelo Binomial. Como indicação, para as aplicações, o modelo Binomial não deve ser aplicado se n/N≥0.05 (Mendenhall, 1994), isto é, só se considera que a população é suficientemente grande, quando a sua dimensão for superior a 20 vezes, a dimensão da amostra seleccionada (Há autores que consideram que ainda se pode aplicar o modelo Binomial se a dimensão da população for superior a 10 vezes a dimensão da amostra seleccionada).
Observação - Considerando ainda o caso de termos uma população suficientemente grande (de acordo com o critério avançado anteriormente), a amostragem com reposição ou sem reposição, são praticamente equivalentes, já que a probabilidade de extrairmos o mesmo elemento duas vezes, quando se considera a reposição, é extremamente pequena.

Exemplos >>

Exemplo 1

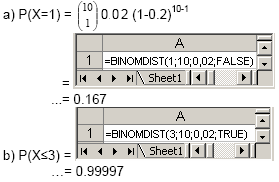
A empresa LHD, de transporte de correio rápido, garante a indemnização dos clientes, cujo correio não chegue ao destino, nas condições contratadas. Apesar de todos os esforços da empresa, no sentido de apresentarem o melhor serviço, através de registos passados, sabe-se que 2% das expedições, não chegam nas condições desejadas. Um banco enviou, através da LHD, 10 envelopes.

a) Qual a probabilidade de um destes 10 envelopes não ter chegado ao destino, nas condições desejadas.

b) Qual a probabilidade de, no máximo, 3 dos envelopes não chegarem ao destino.

Resolução: Representemos por X a v.a. que representa o n.º de envelopes, em 10, que não chegam ao destino. Então X pode ser modelada pelo modelo Binomial, de parâmetros n=10 e p=0.02.

Observação – para calcular as probabilidades anteriores, utilizámos a função do Excel BINOMDIST [DISTRBINOM], em que:


  • Number_s [Num_s] é o número de sucessos;
  • Trials [Tentativas] é o número de provas independentes;
  • Probability_s [Probabilidades_s] é a probabilidade de sucesso em cada prova;
  • Cumulative [Cumulativo] é um valor lógico, tal que: se se utilizar TRUE [Verdadeiro], devolve o valor da probabilidade acumulada, da variável X assumir valores menores ou iguais a Number_s [Num_s]; se se utilizar FALSE [Falso], devolve o valor da f.m.p no ponto Number_s [Num_s].

Exemplo 2

Como exemplo de uma situação que pode ser modelada pelo modelo geométrico, apresentámos na secção 2.4.2 o problema das caixas de cereais. Estávamos, aí, interessados em saber o número médio de caixas até obtermos os 6 prémios diferentes. Suponhamos que um destes 6 prémios é a figura do Batman.

a) Qual a probabilidade de ter de comprar 10 caixas, até obter uma figura do Batman?

b) Qual a probabilidade de em 10 caixas que comprou, ter uma com a figura do Batman?
Resolução
a) Estamos interessados na variável aleatória X, que consiste em saber quantas provas são necessárias, até se obter sucesso, sendo a probabilidade de sucesso 1/6. Então X é bem modelada por um modelo geométrico, pelo que: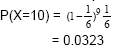

b) Agora estamos interessados na variável aleatória Y, que representa o número de sucessos, em 10 provas, sendo a probabilidade de sucesso 1/6. Então Y é bem modelada pelo modelo Binomial, pelo que: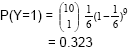

Exemplo 3

O gerente de uma casa que vende material informático fez uma encomenda de 20 impressoras de determinada marca, que será aceite se na inspecção de 3 das impressoras, para ver se funcionam ou estão avariados, não encontrar nenhuma avariada. Quando a encomenda chega o gerente analisa as 3 primeiras impressoras a serem descarregadas.

Embora o gerente não saiba, 2 das impressoras têm avarias. Será que estamos perante uma experiência binomial?

Resolução

Estamos perante uma experiência constituída por 3 provas, em que em cada prova se pode verificar o sucesso (impressora avariada) ou insucesso (impressora boa). A probabilidade de seleccionar uma impressora defeituosa é 2/20, admitindo que qualquer uma das impressoras poderia ter sido colocada no meio de transporte, em melhores condições de ser a primeira a ser descarregada. No entanto as provas não são independentes, já que a probabilidade de obter uma impressora defeituosa na 2ª prova ou na 3ª prova depende do que aconteceu nas provas anteriores, pelo que a probabilidade de sucesso não se mantém constante ao longo das provas. Assim, não estamos perante uma experiência binomial.

Exemplo 4

(adaptado de De Veaux et al, 2004)

Os indivíduos com sangue de tipo O, RH-, são chamados de dadores universais. Só 6% da população tem este tipo de sangue.

a) Em média, quantos dadores espera observar, na unidade móvel que costuma estacionar em Entrecampos, Lisboa, até obter alguém que seja dador universal? Qual a probabilidade de que o primeiro dador universal se encontre entre os 4 primeiros dadores?

b) Suponha que chegam 20 dadores à unidade móvel. Quantos dadores universais espera encontrar? Qual a probabilidade de encontrar 2 ou 3 dadores universais?

Resolução

a) Se representarmos por X o número de dadores até obter 1 que seja dador universal, podemos considerar que X tem uma distribuição geométrica de parâmetro 0.06.
Então E(X) = 1/0.06 = 16.7, pelo que se espera examinar em média 16.7 pessoas até encontrar um dador universal.

A probabilidade de que se encontre um dador de tipo O-, nos 4 primeiros é dada por P(X=1) +P(X=2)+P(X=3)+P(X=4) = 0.2193.

Cerca de 22% das vezes encontra-se um dador universal nos primeiros 4 dadores que se apresentam.

b) Se representarmos por Y o número de dadores universais em 20, Y tem uma distribuição Binomial de parâmetros 20 e 0.06. Então E(Y) = 20×0.06 = 1.2 e
P(Y = 2 ou 3) = P(Y = 2) + P(Y = 3) = 0.3106.

Exemplo 5

Um indivíduo faz anos em Junho. Resolve, na rua, perguntar às pessoas que encontra, qual o mês em que fazem anos, até encontrar uma que faça anos no mesmo mês.

a) Qual a probabilidade de ter de importunar 10 pessoas? Em média a quantas pessoas tem de fazer a pergunta, até encontrar uma a fazer anos no mesmo mês?

b) E se pretender encontrar 2 pessoas a fazerem anos em Junho, em vez de 1, qual a probabilidade de ter de perguntar a 10 pessoas?

Resolução
a) Seja X a v.a. que representa o número de pessoas a quem tem de importunar, para encontrar 1 a fazer anos em Junho. Então podemos utilizar o modelo geométrico em que a probabilidade de sucesso é 1/12, se admitirmos que existe igual probabilidade de fazer-se anos em qualquer um dos 12 meses, donde
P(X = 10) = (11/12)9 х1/12 = 0.038. Neste caso E(X) = 12, pelo que, em média, terá de perguntar a 12 pessoas, até encontrar 1 a fazer anos no mesmo mês.

b) Seja Y a variável que representa o número de pessoas a quem tem de importunar, até encontrar 2 a fazer anos no mesmo mês – sucesso (S). Então, para que o segundo sucesso se verifique na enésima prova (Y=n), é necessário que nas (n-1) provas anteriores se verifique 1 sucesso e que na enésima prova se verifique o 2º sucesso, de acordo com o seguinte esquema:

Nota – Representando por Z a variável aleatória que dá o número de provas necessárias para se verificar o k-ésimo sucesso, em que a probabilidade de sucesso é p, verifique que a probabilidade de o k-ésimo sucesso se verificar na enésima prova vem igual a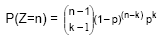


Comentário – Não confunda as situações em que pode aplicar o modelo geométrico e o modelo binomial! Embora ambos pressuponham que estamos em presença de provas independentes, em que em cada prova se pode verificar sucesso ou insucesso, sendo constante a probabilidade de sucesso (provas de Bernoulli):

  • Quando estamos interessados em saber quantas provas são necessárias para se verificar sucesso pela 1ª vez, utilizamos o modelo geométrico;
  • Quando estamos interessados em saber quantos sucessos se verificam num número especificado de provas, utilizamos o modelo binomial.