
Esta tarefa destina-se a alunos do 10.º ano de escolaridade e nela propõe-se a abordagem no tema ESTATÍSTICA, do tópico Dados quantitativos bivariados e dos subtópicos Diagrama de dispersão, Coeficiente de correlação linear e Reta de regressão. Privilegia-se ainda a interpretação de gráficos.
O texto seguinte foi publicado no dia 14 de novembro de 2023, o Dia Nacional da Igualdade Salarial, em Portugal. Esta data não é fixa, pois representa o número de dias de trabalho em que as mulheres deixam, simbolicamente e em média, de receber os seus salários, enquanto os homens continuam a ser remunerados.
Segundo os dados mais recentes disponíveis na edição de 2023 do Barómetro das Diferenças Remuneratórias entre Mulheres e Homens, do Gabinete de Estratégia e Planeamento do Ministério do Trabalho, Solidariedade e Segurança Social, a diferença salarial entre homens e mulheres equivale a 48 dias de trabalho pagos aos homens, mas não remunerados às mulheres. Embora a disparidade salarial de género tenha vindo a diminuir, de 17,9% em 2010 para 13,1% em 2021...
Com o objetivo de combater essa situação, têm vindo a ser implementadas e fortalecidas iniciativas, estratégias e ações para estimular a equidade salarial entre homens e mulheres. Um exemplo dessas ferramentas é a norma NP 4588:2023 – Sistema de gestão para a equidade salarial entre mulheres e homens – Requisitos e diretrizes. A norma estabelece os critérios necessários para que uma organização implemente, mantenha e administre um sistema de gestão destinado a eliminar a disparidade salarial com base no género e promover a igualdade salarial entre mulheres e homens no emprego...
A Comissão Europeia também assinala, anualmente, desde 2016, o Dia Europeu da Igualdade Salarial, com o propósito de sensibilizar para o facto de as trabalhadoras na Europa ainda ganharem, em média, menos do que os seus colegas homens. Este dia muda todos os anos, com o mesmo critério do dia nacional relativo ao mesmo assunto; ou seja, a data depende dos números mais recentes sobre as disparidades salariais entre homens e mulheres. Em 2023 o «European Equal Pay Day» assinalou-se a 15 de novembro... Em Portugal o «Dia Nacional da Igualdade Salarial» foi assinalado a 14 de novembro.
Ainda em Portugal e com financiamento maioritariamente europeu, proveniente do Fundo Social Europeu Mais, o “programa PESSOAS 2030” vai apoiar medidas de promoção da igualdade de género, designadamente de combate à segregação profissional e de mitigação do gap salarial de género. Até 2029, o Programa pretende apoiar 75 000 raparigas, ou mulheres e rapazes ou homens em ações de desconstrução dos estereótipos profissionais de género, no âmbito do projeto engenheiras por um dia. O objetivo é conseguir que pelo menos 65% das raparigas ou mulheres demonstrem interesse em estudar e/ou trabalhar nas áreas STEAM (ciência, tecnologia, engenharia, artes e matemática) ou TIC (tecnologias de informação e comunicação), no final da participação nestas ações.
1. Formule uma questão estatística que lhe permita estudar o tema relacionado com o texto anterior.
2. Indique uma variável estatística que lhe permita estudar a questão estatística formulada no ponto anterior.
No que segue, considera-se como questão estatística o estudo da evolução da «diferença entre o salário médio dos homens e o salário médio das mulheres, ao longo dos anos», na população portuguesa. Para essa questão, uma variável estatística possível é «o valor, em percentagem, que a remuneração média mensal dos homens é superior à das mulheres, em cada ano», a que se poderá dar o nome de «Disparidade salarial entre homens e mulheres» (Disp.sal).
3. Recolha de dados – Para estudar a evolução da «disparidade salarial entre homens e mulheres», ao longo dos anos, considere a seguinte tabela obtida da página da PORDATAi , com a remuneração base média mensal dos trabalhadores por conta de outrem, por sexo, de 1985 a 2022:
Remuneração base média mensal, em euros, dos trabalhadores por conta de outrem por sexoii
| Ano | Masc | Fem |
|---|---|---|
| 1985 | 160,9 | 125,4 |
| 1986 | 192,0 | 149,9 |
| 1987 | 220,6 | 172,2 |
| 1988 | 243,6 | 189,6 |
| 1989 | 276,4 | 212,8 |
| 1990 | x | x |
| 1991 | 382,5 | 290,7 |
| 1992 | 438,3 | 332,3 |
| 1993 | 486,2 | 371,5 |
| 1994 | 523,0 | 407,7 |
| 1995 | 542,8 | 416,8 |
| 1996 | 573,7 | 442,9 |
| 1997 | 589,5 | 454,1 |
| 1998 | 624,7 | 479,3 |
| 1999 | 648,7 | 497,4 |
| 2000 | 674,7 | 523,6 |
| 2001 | x | x |
| 2002 | 744,2 | 599,5 |
| 2003 | 775,9 | 620,1 |
| 2004 | 805,5 | 645,3 |
| 2005 | 832,5 | 672,0 |
| 2006 | 857,6 | 691,4 |
| 2007 | 876,8 | 712,7 |
| 2008 | 916,3 | 747,7 |
| 2009 | 940,5 | 773,5 |
| 2010 | 976,7 | 800,8 |
| 2011 | 984,2 | 807,5 |
| 2012 | 999,0 | 813,7 |
| 2013 | 993,2 | 815,6 |
| 2014 | 985,0 | 820,3 |
| 2015 | 990,1 | 825,0 |
| 2016 | 997,4 | 840,3 |
| 2017 | 1012,3 | 861,2 |
| 2018 | 1039,1 | 888,6 |
| 2019 | 1073,8 | 922,6 |
| 2020 | 1109,2 | 960,3 |
| 2021 | 1152,2 | 999,3 |
| 2022 | 1217,3 | 1.054,4 |
x “valor em falta”
(ii) Remuneração média mensal, sem especificação do tipo de trabalho
4. Análise dos dados, a partir da tabela anterior:
4.1. Faça uma representação gráfica adequada para mostrar a evolução da remuneração média mensal, por sexo, de 1985 a 2022. Comente-a.
4.2. Acrescente à tabela uma nova coluna obtida da seguinte forma: para cada ano, considere o valor obtido a partir da expressão:
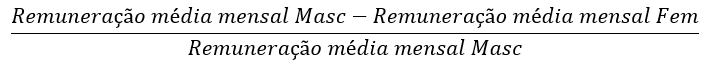
Considere os valores em %. Atendendo à questão estatística e à variável estatística escolhidas, acha que um nome adequado para esta coluna poderá ser Disparidade salarial entre homens e mulheres?
O valor obtido para a Disparidade salarial entre homens e mulheres é, para o ano de 2010, igual a 18%. Explique o significado deste valor.
5. Utilizando a tecnologia, represente num diagrama de dispersão os dados referentes ao par de variáveis Ano e Disparidade salarial entre homens e mulheres. Qual das variáveis deve ser considerada como explanatória?
5.1. Tendo em consideração a forma da “nuvem de pontos” no diagrama de dispersão, tem sentido ajustar um modelo linear a esses pontos? Se respondeu sim, utilize a tecnologia para calcular o coeficiente de correlação linear e ajustar uma reta de regressão linear.
5.2. Interprete o coeficiente de correlação quanto à força e à direção com que as variáveis se associam.
5.3. Na tabela, faltam os dados referentes aos anos de 1990 e 2001. Utilize a equação da reta de regressão para estimar os valores da Disparidade salarial entre homens e mulheres para estes dois anos.
5.4. Utilizando a mesma metodologia que utilizou na alínea anterior, pode estimar o valor da disparidade salarial para 2030?
6. Faça uma pequena reflexão sobre os resultados a que chegou neste estudo.
Proposta de resolução
4.1. Uma representação gráfica adequada é o gráfico de linhas, que mostra a evolução, ao longo dos anos, da remuneração média mensal dos homens e das mulheres:
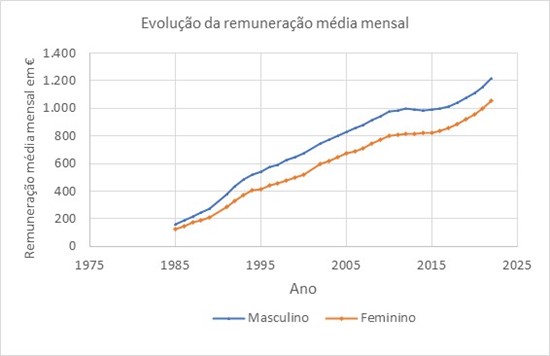
Comentários:
- Na representação gráfica anterior, é notório o aumento da remuneração média mensal, de 1985 até 2022, quer para os homens, quer para as mulheres.
- No que respeita à desigualdade salarial ao longo dos anos, o gráfico transmite a ideia de que essa desigualdade, ao longo do tempo, tem aumentado ou se manteve, o que contraria o texto introdutório. Será que o gráfico é enganador?
- O gráfico é enganador, já que o efeito apontado anteriormente é provocado pelo facto de as grandezas dos valores em estudo ser muito diferente ao longo dos anos. Por exemplo, uma diferença salarial de cerca de 90€ em 1991, no qual o salário médio mensal dos homens era aproximadamente 380€ e o das mulheres aproximadamente 290€, era mais penalizadora para as mulheres que auferiam cerca de 76% do salário dos homens, do que uma diferença de cerca de 177€, em 2011, quase o dobro da de 1991, mas no qual as mulheres auferiam cerca de 82% do salário dos homens.
4.2. Tendo em consideração a forma como foi construída a coluna que nos dá «o valor da diferença, em percentagem, entre a remuneração média mensal dos homens, e a remuneração média mensal das mulheres», tem sentido falar em «disparidade salarial entre homens e mulheres». Com a nova coluna, tem-se:
Remuneração base média mensal, em euros, dos trabalhadores por conta de outrem por sexo
| Ano | Masc | Fem | Disp.Sal. |
|---|---|---|---|
| 1985 | 160,9 | 125,4 | 22% |
| 1986 | 192,0 | 149,9 | 22% |
| 1987 | 220,6 | 172,2 | 22% |
| 1988 | 243,6 | 189,6 | 22% |
| 1989 | 276,4 | 212,8 | 23% |
| 1990 | x | x | |
| 1991 | 382,5 | 290,7 | 24% |
| 1992 | 438,3 | 332,3 | 24% |
| 1993 | 486,2 | 371,5 | 24% |
| 1994 | 523,0 | 407,7 | 22% |
| 1995 | 542,8 | 416,8 | 23% |
| 1996 | 573,7 | 442,9 | 23% |
| 1997 | 589,5 | 454,1 | 23% |
| 1998 | 624,7 | 479,3 | 23% |
| 1999 | 648,7 | 497,4 | 23% |
| 2000 | 674,7 | 523,6 | 22% |
| 2001 | x | x | |
| 2002 | 744,2 | 599,5 | 19% |
| 2003 | 775,9 | 620,1 | 20% |
| 2004 | 805,5 | 645,3 | 20% |
| 2005 | 832,5 | 672,0 | 19% |
| 2006 | 857,6 | 691,4 | 19% |
| 2007 | 876,8 | 712,7 | 19% |
| 2008 | 916,3 | 747,7 | 18% |
| 2009 | 940,5 | 773,5 | 18% |
| 2010 | 976,7 | 800,8 | 18% |
| 2011 | 984,2 | 807,5 | 18% |
| 2012 | 999,0 | 813,7 | 19% |
| 2013 | 993,2 | 815,6 | 18% |
| 2014 | 985,0 | 820,3 | 17% |
| 2015 | 990,1 | 825,0 | 17% |
| 2016 | 997,4 | 840,3 | 16% |
| 2017 | 1012,3 | 861,2 | 15% |
| 2018 | 1039,1 | 888,6 | 14% |
| 2019 | 1073,8 | 922,6 | 14% |
| 2020 | 1109,2 | 960,3 | 13% |
| 2021 | 1152,2 | 999,3 | 13% |
| 2022 | 1217,3 | 1.054,4 | 13% |
O valor de 18% significa que a remuneração média mensal dos homens era, em 2010, superior em 18% à das mulheres, ou que a remuneração média mensal das mulheres era 82% da remuneração média mensal dos homens.
5. A variável explanatória é o tempo, aqui referido por Ano, pelo que se apresenta a seguir o diagrama de dispersão do par de variáveis (Ano, Disp.Sal.)
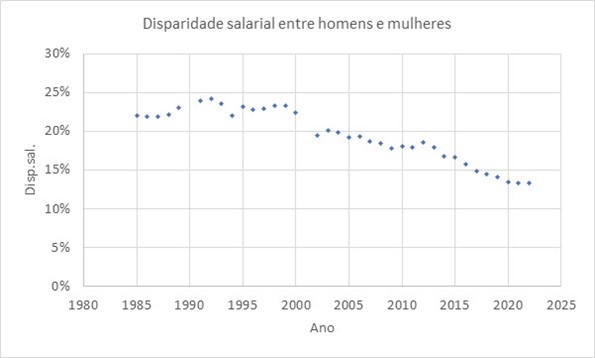
5.1. O diagrama de dispersão anterior, que foi construído no Excel, mostra que os dados se dispõem de forma aproximadamente linear, pelo que se introduz a equação da reta de regressão e o valor do coeficiente de correlação ao quadrado, r2 (chamado coeficiente de determinação e que traduz a qualidade do ajustamento):
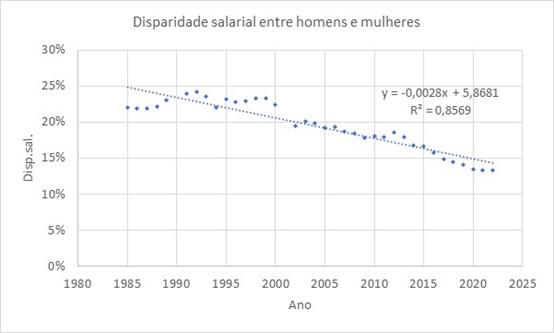
em que x – Ano e y – Disp.sal..
5.2. Sendo r2 = 0,8568, o coeficiente de correlação é igual a cerca de -0,93 o que significa uma associação forte e negativa entre as variáveis em estudo, ou seja, a disparidade salarial entre homens e mulheres apresentou uma tendência no sentido da redução no período temporal analisado.
5.3. Utilizando a equação da reta de regressão dada pelo Excel, disparidade salarial = - 0,0028 × ano + 5,8681, com o ano igual a 1990 e 2001, obtêm-se para a disparidade salarial os valores 29,6% e 26,5%, respetivamente. No entanto, tendo em consideração o gráfico com a reta de regressão, os valores de que estaríamos à espera seriam aproximadamente 23,5% e 20,5%, bem diferentes dos estimados a partir da reta de regressão. Qual a razão desta discrepância? Esta situação resulta de um problema de falta de precisão, devido ao facto de a variável explanatória ter 4 dígitos (significativos) e o número de dígitos (significativos) do declive ser só 2 (os zeros à esquerda não contam). Assim, recalculou-se a reta de regressão, optando por considerar mais casas decimais, para que o declive também apresente quatro dígitos, sem contar com os zeros à esquerda:
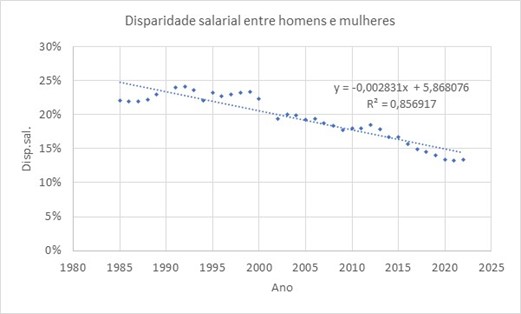
Recalculando os valores estimados para os anos de 1990 e 2001, obtém-se como estimativas para a disparidade salarial 23,4% e 20,3%, respetivamente.
5.4. Não se pode estimar o valor da disparidade salarial para o ano de 2030, porque este valor está fora do intervalo dos valores considerados para a regressão.
6. Deixa-se ao critério de cada um fazer a sua reflexão. No entanto seria importante referir que os dados utilizados se referem às remunerações médias mensais para trabalhadores por conta de outrem, sem entrar em linha de conta com o tipo de profissão e o tipo de qualificação. Na verdade, se se considerar trabalhadores com formação superior, a disparidade salarial ronda os 26%, o que poderá ter a ver com as áreas STEAM, referidas na Introdução, nas quais os salários são altos, mas a representatividade das mulheres é baixa.











.png)
