Índice | 
II. Experiência aleatória | 
IV. Modelos de Probabilidade discretos e contínuos
III. Probabilidade
Parte 34 de 47
8. Definição Axiomática de Probabilidade
(Esta secção baseia-se nas folhas elaboradas por Luísa Loura e Maria Eugénia Graça Martins, para o Projecto Reanimat, Junho 2003).
Considere-se então um espaço de resultados S e uma classe W de subconjuntos de S (acontecimentos). Admite-se que W satisfaz as seguintes condições:
- Se um acontecimento A está em W, então o seu complementar também está em W;
- Se dois acontecimentos A e B estão em W, então a sua união também está em W;
- S está em W.
Dado o par (S, W), a cada elemento AÎW, associa-se um número que se chama Probabilidade e se representa por P(A).
As probabilidades associadas aos acontecimentos de uma mesma família de acontecimentos W, satisfazem as seguintes propriedades ou axiomas:
Axioma 1 - Para qualquer elemento AÎW, P(A)³0
Axioma 2 - P(S) = 1
Axioma 3 - Se os acontecimentos A e B são disjuntos, isto é, AÇB= Æ, então P(AÈB) = P(A) + P(B)
Será que o modelo de Laplace e o modelo frequencista satisfazem a axiomática que acabámos de apresentar? Efectivamente assim é, como pode verificar carregando no botão respectivo.
Modelo de Laplace
Modelo de Laplace como modelo da axiomática de probabilidade
O espaço de resultados S para o modelo de Laplace é sempre um conjunto finito, não vazio, S={s1,s2,...,sk}. Sabemos ainda que dado um subconjunto A de S a probabilidade de ocorrência de A é dada por nº de casos favoráveis a A/ nº de casos possíveis ou, em termos de cardinais de conjuntos, P(A)=#A/#S. Note-se que uma consequência imediata desta regra de cálculo das probabilidades para o modelo de Laplace é que a probabilidade de cada acontecimento elementar Ei={si} é igual a 1/k.
Demonstremos então que P verifica os axiomas A1, A2 e A3:
P(A) é o quociente entre um número inteiro não negativo e um número inteiro positivo sendo por isso um número (racional) não negativo (o cardinal de um conjunto finito é sempre um número inteiro não negativo).
Logo A1 verifica-se.
· P(S) = 
=1.
Logo A2 verifica-se.
· 
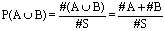se os conjuntos A e B forem disjuntos.
Logo, para A e B disjuntos,
· 
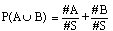= P(A) + P(B) pelo que A3 também se verifica.
Modelo frequencista
Modelo frequencista como modelo da axiomática da probabilidade
Suponhamos que ao realizar N vezes uma experiência aleatória se obteve os seguintes resultados:
| Resultados | Frequências |
|---|---|
| S1 | N1 |
| S2 | N2 |
| ... | ... |
| Sk | Nk |
No modelo frequencista da probabilidade começamos por considerar um conjunto S que contenha os resultados observados {s1,s2,...,sk}. Em cada realização da experiência diz-se que um acontecimento A ocorreu se o resultado da experiência for algum dos seus elementos. Numa primeira fase considere-se que a probabilidade de ocorrência do acontecimento A é dada por
Com esta definição os acontecimentos elementares {si}, i=1,2,...,k têm probabilidade Ni/N, onde representamos por Ni a frequência absoluta com que se verificou {si}, e qualquer outro elemento de S terá probabilidade nula. Assim sendo o espaço S poderá não ser equiprovável. Vejamos agora que uma probabilidade definida por este processo verifica a axiomática anteriormente apresentada:
Modelo frequencista como modelo da axiomática da probabilidade (cont.)
O nº de vezes que A ocorreu é sempre um inteiro não negativo. Logo PN(A)³0 e A1 verifica-se.
Em cada realização da experiência S ocorreu sempre, uma vez que S contém todos os resultados observados. Logo PN(S) = 
=1 e A2 verifica-se.
Dados dois conjuntos disjuntos A e B, em cada realização da experiência se A ocorre é porque se obteve como resultado um dos elementos de A e, como tal, B não ocorre e vice-versa. Por outro lado, dizer que ocorre a reunião de A com B é dizer que se obteve como resultado um elemento si que ou está em A ou está em B mas não nos dois em simultâneo. Assim sendo cada ocorrência de A contribui com um incremento de uma unidade no nº de ocorrências de (AÈB) o mesmo acontecendo com cada ocorrência de B. O nº total de ocorrências de (AÈB) será então a soma do nº total de ocorrências de A com o nº total de ocorrências de B o que prova que A3 também se verifica.
A definição frequencista de probabilidade diz-nos que P(A) é o limite de PN(A) quando N tende para infinito. Admitindo que se deu um sentido preciso à palavra "limite" e que esse "limite" verifica as propriedades usuais é agora fácil de verificar que também aqui se tem a validade dos três axiomas. Na verdade para mostrar que se tem A3 basta utilizar o facto do limite da soma ser a soma dos limites. O axioma A2 é imediato pois a sucessão PN(S) é constante, igual a 1. Para provar A1 basta notar que se uma sucessão é sempre não negativa então o seu limite também é não negativo.
.png "Instituto Nacional de Estatística"){kind=logo}
