Noções de probabilidades
Noções de Probabilidades
 Índice |
Índice |  II. Experiência Aleatória
II. Experiência Aleatória
Introdução (Cont.)
Parte 3 de 3
Por outro lado, no módulo de Estatística foi chamada a atenção que para interpretar correctamente os resultados de análises estatísticas necessitamos de alguns conhecimentos probabilísticos. Esta situação surge quando pretendemos fazer Inferência Estatística, isto é, quando pretendemos tirar conclusões acerca de um grande conjunto de indivíduos, baseando-nos num número restrito desses indivíduos. Foi neste contexto que foram definidos os conceitos de População e Amostra nesse módulo.
É a probabilidade que nos vai permitir quantificar esta incerteza, quando passamos do particular (Amostra) para o geral (População) na medida em que quantifica o erro cometido ao tomarmos determinadas decisões.
Para definir o conceito de probabilidade, vamos introduzir alguma terminologia. A primeira definição a ser introduzida, vai ser a de experiência aleatória.
Noções de Probabilidades
 Índice |
Índice |  II. Experiência Aleatória
II. Experiência Aleatória
Introdução (Cont.)
Parte 2 de 3
Nas situações consideradas anteriormente em que somos conduzidos a utilizar a noção de probabilidade, e noutras situações da vida real em várias áreas científicas, estamos perante fenómenos não determinísticos, pois quando se realizam não temos a certeza do que é que se vai observar.
Quando apostamos no totoloto podemos jogar num número razoavelmente grande de chaves e só uma é que é a que nos permite ganhar; quando olhamos para o céu e não vemos nuvens, dizemos que não vai chover, porque a experiência anterior nos diz que em situações idênticas, não é costume chover; quando um doente é tratado com um novo medicamento pode ficar curado ou não; quando um político se candidata a determinadas eleições o número de eleitores que vai votar nele é desconhecido.
Cada uma destas situações pode ser considerada um fenómeno aleatório, por oposição aos fenómenos determinísticos, cujos resultados se conseguem prever.
A Teoria da Probabilidade prende-se com o estudo de modelos matemáticos especiais, a que chamamos modelos probabilísticos, para descrever fenómenos aleatórios.
NOÇÕES DE PROBABILIDADES
 Índice |
Índice |  III. Probabilidade |
III. Probabilidade |  V. Exercícios
V. Exercícios
IV. Modelos de probabilidade contínuos
Parte 77 de 78
|
Para dar uma ideia da concentração da distribuição normal, em torno do seu valor médio, apresentamos seguidamente algumas probabilidades: |
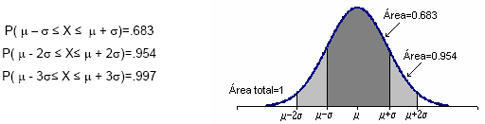 |
|
À distribuição normal que tem valor médio 0 e desvio padrão 1 chamamos distribuição "standard " ou reduzida, e representamos por 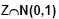 . . |
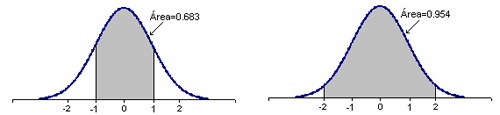 |
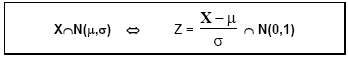 Se a v.a. X tiver valor médio Se a v.a. X tiver valor médio 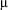 e desvio padrão e desvio padrão 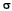 , então a v.a. , então a v.a. 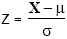 , tem valor médio 0 e desvio padrão 1. , tem valor médio 0 e desvio padrão 1. |
|
|
NOÇÕES DE PROBABILIDADES
 Índice |
Índice |  III. Probabilidade |
III. Probabilidade |  V. Exercícios
V. Exercícios
IV. Modelos de probabilidade contínuos
Parte 78 de 78
|
Propriedade |
| Da simetria da curva normal, deduz-se imediatamente a seguinte propriedade: |
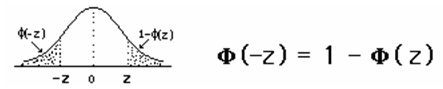 |
|
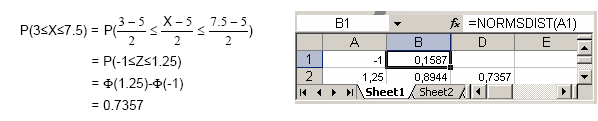
Para calcular as probabilidades referentes à Normal, podemos utilizar, quer a máquina de calcular, quer o computador, através da folha de cálculo Excel. Exemplificamos a seguir alguns cálculos, utilizando o Excel. |
NOÇÕES DE PROBABILIDADES
 Índice |
Índice |  III. Probabilidade |
III. Probabilidade |  V. Exercícios
V. Exercícios
IV. Modelos de probabilidade contínuos
Parte 76 de 78
|
Vejamos algumas propriedades, relativamente à representação gráfica, da função densidade normal, que se deduzem da sua expressão analítica (que não apresentamos por sair fora do âmbito deste curso): |
||
|
||
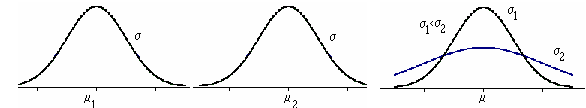 |
||
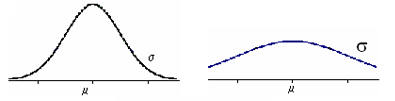 Se deixasse cair um peso em cima da curva da função densidade, ela ficaria mais achatada, o que implicaria um maior desvio padrão! |









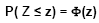 .
.




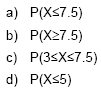





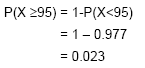



.png)
